07204 Pareto-Diagramm
|
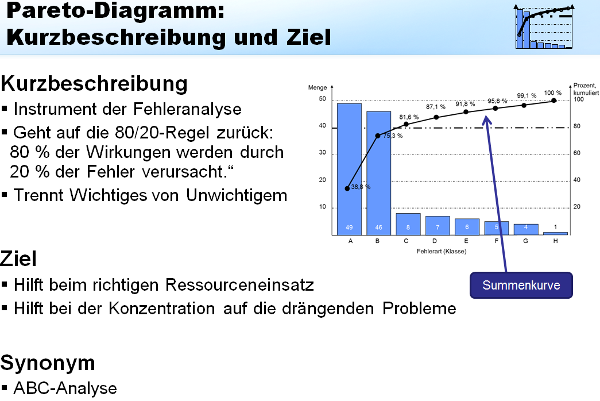
Das Pareto-Diagramm wird oft zur Fehleranalyse eingesetzt. Es sortiert Fehler bzw. Probleme nach deren Relevanz in absteigender Reihenfolge und stellt sie als Balkendiagramm zusammen mit der Summenkurve ihrer Bedeutung dar. Die Darstellung hilft, sich auf die wesentlichen Qualitätsprobleme zu konzentrieren, um so Verschwendung zu bekämpfen (s. Kap. 07201). Arbeitshilfen: von: |
1 Ziel und Kurzbeschreibung
Kurzbeschreibung
Das Pareto-Diagramm geht auf den italienischen Nationalökonomen Vilfredo Pareto und dessen 80/20-Regel zurück. Nach dieser Regel werden 80 % der Auswirkungen durch lediglich 20 % der Ursachen hervorgerufen. Das Pareto-Diagramm macht diese besonders beachtenswerten 20 %-Ursachen sichtbar.
Das Pareto-Diagramm geht auf den italienischen Nationalökonomen Vilfredo Pareto und dessen 80/20-Regel zurück. Nach dieser Regel werden 80 % der Auswirkungen durch lediglich 20 % der Ursachen hervorgerufen. Das Pareto-Diagramm macht diese besonders beachtenswerten 20 %-Ursachen sichtbar.
Dazu werden die unterschiedlichen Ursachen bzw. Fehler mit der Häufigkeit ihres Auftretens erfasst, gegebenenfalls mit den von ihnen verursachten Kosten gewichtet und anschließend in zahlen- bzw. wertmäßig absteigender Reihenfolge sortiert.
Die Fehler lassen sich nun in dieser Sortierung in ein Diagramm übertragen: Zunächst wird je Fehler durch einen Balken die Häufigkeit seines Auftretens bzw. seine Kostenwirkung dargestellt. Weiter links im Diagramm stehende Fehler sind bedeutsamer als die rechts genannten.
Die Darstellung wird durch eine Summenkurve ergänzt. Diese entsteht, indem man die prozentuale Bedeutung jedes Fehlers zur Gesamtbedeutung kumuliert und die Werte einzeichnet.
Ziel
Das Pareto-Diagramm wird angefertigt, um Wichtiges von Unwichtigem zu trennen. Es hilft, sich auf die wesentlichen Ursachen für ein Qualitätsproblem und dessen Auswirkungen zu konzentrieren.
Das Pareto-Diagramm wird angefertigt, um Wichtiges von Unwichtigem zu trennen. Es hilft, sich auf die wesentlichen Ursachen für ein Qualitätsproblem und dessen Auswirkungen zu konzentrieren.
Anwendungsgebiet
Anwendungsfälle für das Pareto-Diagramm sind:
Anwendungsfälle für das Pareto-Diagramm sind:
| • | Erkennen der Wichtigkeit einzelner Ursachen und Identifikation wesentlicher Ansatzpunkte, |
| • | Festlegung von Prioritäten für weitere Maßnahmen. |
Synonyme
Das Pareto-Diagramm wird auch außerhalb des Qualitätsmanagements eingesetzt. In den Bereichen Logistik und Materialwirtschaft wird es auch als ABC-Analyse bezeichnet.
Das Pareto-Diagramm wird auch außerhalb des Qualitätsmanagements eingesetzt. In den Bereichen Logistik und Materialwirtschaft wird es auch als ABC-Analyse bezeichnet.
2 Durchführung
Die Erstellung eines Pareto-Diagramms verläuft in klar abgegrenzten Schritten: Zunächst werden die Daten erhoben. In einem zweiten Schritt werden sie aufbereitet. Dazu werden sie eventuell mit Kosten gewichtet und dann absteigend sortiert. Im folgenden Schritt wird die relative Bedeutung der Fehler ermittelt, damit anschließend im vierten Schritt das Diagramm mit seinen Balken und der Summenkurve gezeichnet werden kann. Der letzte Schritt besteht aus der Klassifizierung von wesentlichen und weniger wichtigen Ursachen.
2.1 Datenherkunft
Fehlersammelkarte
Die Ausgangsdaten für das Diagramm können beispielsweise einer Fehlersammelkarte entnommen werden. Dieses Instrument zur Fehlererfassung notiert alle Fehler mit der Häufigkeit ihres Auftretens und stellt damit eine ideale Quelle für die Datenherkunft dar.
Die Ausgangsdaten für das Diagramm können beispielsweise einer Fehlersammelkarte entnommen werden. Dieses Instrument zur Fehlererfassung notiert alle Fehler mit der Häufigkeit ihres Auftretens und stellt damit eine ideale Quelle für die Datenherkunft dar.
Andere Quellen
Neben der Fehlersammelkarte eignen sich auch alle anderen Datenquellen, die eine Einteilung des Grundproblems in verschiedene Kategorien ermöglichen und diesen die jeweilige Häufigkeit zuweisen. Zu denken ist hier an die Berichte des Kundendienstes oder an Reklamationsscheine, die sich hinsichtlich der Fehler auswerten lassen.
Neben der Fehlersammelkarte eignen sich auch alle anderen Datenquellen, die eine Einteilung des Grundproblems in verschiedene Kategorien ermöglichen und diesen die jeweilige Häufigkeit zuweisen. Zu denken ist hier an die Berichte des Kundendienstes oder an Reklamationsscheine, die sich hinsichtlich der Fehler auswerten lassen.
Genaue Regeln
Werden die grundlegenden Daten aus den genannten anderen Quellen erhoben, ist für diese Form der Sekundärerhebung genau zu regeln, wie Fehler einzelnen Kategorien zugeordnet werden. Es ist wichtig, dass alle an der Erhebung beteiligten Personen das gleiche Verständnis der Fehlerkategorien besitzen. Nur so kann die Objektivität der Daten gewährleistet werden.
Werden die grundlegenden Daten aus den genannten anderen Quellen erhoben, ist für diese Form der Sekundärerhebung genau zu regeln, wie Fehler einzelnen Kategorien zugeordnet werden. Es ist wichtig, dass alle an der Erhebung beteiligten Personen das gleiche Verständnis der Fehlerkategorien besitzen. Nur so kann die Objektivität der Daten gewährleistet werden.
Anzahl Kategorien
Für eine „richtige” Anzahl von Kategorien kann keine generelle Aussage getroffen werden. Ziel des Pareto-Diagramms ist es, die wesentlichen Kategorien zu identifizieren. Daher zeigt die Anwendung erst ab einer Untergrenze von sieben bis zehn Kategorien den Nutzen der Technik. Eine praktische Obergrenze liegt wegen der zunehmenden Unübersichtlichkeit des Diagramms bei ca. 30 Kategorien. Sollten mehr Kategorien vorliegen, ist deren weitere Gruppierung und Verdichtung zu überlegen.
Für eine „richtige” Anzahl von Kategorien kann keine generelle Aussage getroffen werden. Ziel des Pareto-Diagramms ist es, die wesentlichen Kategorien zu identifizieren. Daher zeigt die Anwendung erst ab einer Untergrenze von sieben bis zehn Kategorien den Nutzen der Technik. Eine praktische Obergrenze liegt wegen der zunehmenden Unübersichtlichkeit des Diagramms bei ca. 30 Kategorien. Sollten mehr Kategorien vorliegen, ist deren weitere Gruppierung und Verdichtung zu überlegen.
2.2 Datenaufbereitung
Gewichtung der Fehler
Der Fehler mit der größten Häufigkeit des Auftretens ist nicht immer der wichtigste Ansatzpunkt: Man denke an eine häufig auszuführende Nacharbeit, die jedoch nur geringe Kosten verursacht, und im Vergleich dazu an einen seltenen, aber wirtschaftlich bedeutsamen Totalverlust des Werkstücks.
Der Fehler mit der größten Häufigkeit des Auftretens ist nicht immer der wichtigste Ansatzpunkt: Man denke an eine häufig auszuführende Nacharbeit, die jedoch nur geringe Kosten verursacht, und im Vergleich dazu an einen seltenen, aber wirtschaftlich bedeutsamen Totalverlust des Werkstücks.
Finanzielle Bewertung
Die unterschiedlichen Folgen können mit einer finanziellen Bewertung der Fehler berücksichtigt werden. Das Diagramm selbst wird dann nicht mit den Häufigkeiten der Fehler, sondern mit den durch den Fehler verursachten Kosten erstellt. Dazu sind die Fehler mit ihrem monetären Schaden zu bewerten. Aus dem Mengengerüst der Fehlerhäufigkeiten und der finanziellen Bewertung ergibt sich durch Multiplikation der Schaden bzw. die finanzielle Bedeutung.
Die unterschiedlichen Folgen können mit einer finanziellen Bewertung der Fehler berücksichtigt werden. Das Diagramm selbst wird dann nicht mit den Häufigkeiten der Fehler, sondern mit den durch den Fehler verursachten Kosten erstellt. Dazu sind die Fehler mit ihrem monetären Schaden zu bewerten. Aus dem Mengengerüst der Fehlerhäufigkeiten und der finanziellen Bewertung ergibt sich durch Multiplikation der Schaden bzw. die finanzielle Bedeutung.
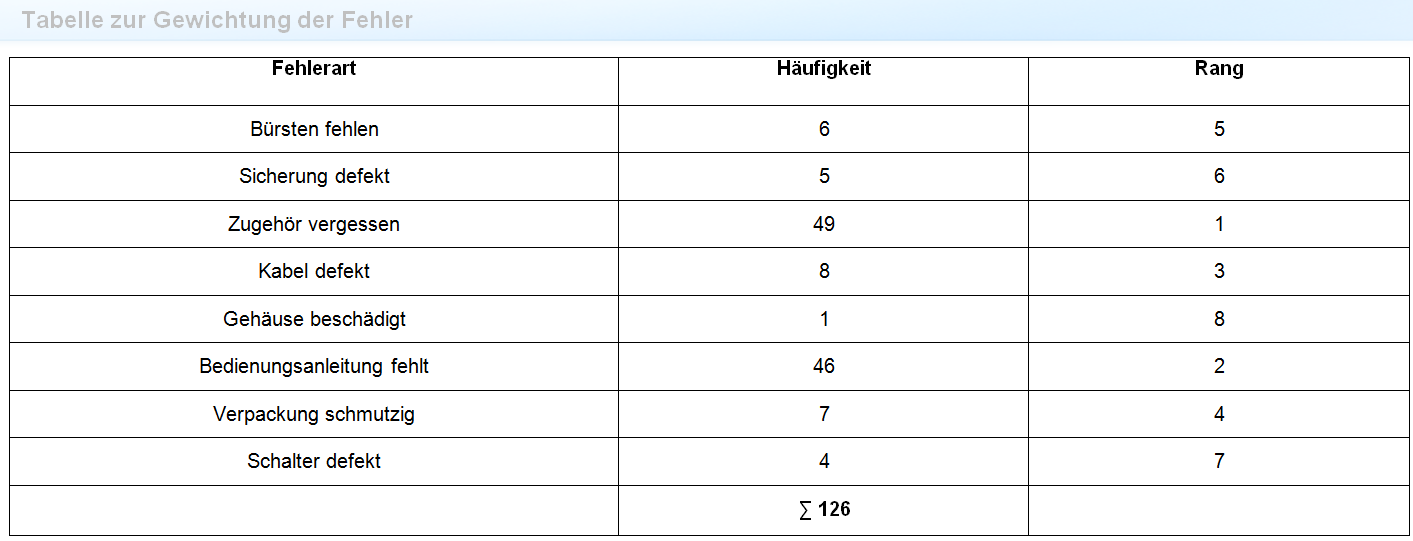
Da die Werte anschließend sortiert werden müssen, bietet sich eine tabellarische Aufbereitung an – siehe Tabelle 1. Sie finden diese Tabelle auch als editierbare Arbeitshilfe zum Download.[ 07204_a.docx]
07204_a.docx]
 07204_a.docx]
07204_a.docx]Tabelle 1: Tabelle zur Gewichtung der Fehler
Fehlerart | Häufigkeit | Rang |
|---|---|---|
Bürsten fehlen | 6 | 5 |
Sicherung defekt | 5 | 6 |
Zubehör vergessen | 49 | 1 |
Kabel defekt | 8 | 3 |
Gehäuse beschädigt | 1 | 8 |
Bedienungsanleitung fehlt | 46 | 2 |
Verpackung schmutzig | 7 | 4 |
Schalter defekt | 4 | 7 |
Σ 126 |
Für die Sortierung ist die Spalte „Rang” zuständig. Die in dieser Spalte gemachten Eintragungen richten sich entweder nach der Häufigkeit der Fehlerart oder – sofern eine finanzielle Bewertung erforderlich ist – nach dem Schaden der Fehlerart. Der größte Wert erhält den Rang „1”, der zweitgrößte den Rang „2” usw.
Das Beispiel in Abbildung 1 enthält keine finanzielle Bewertung. Die Reihung erfolgt daher anhand der Häufigkeiten:
In der letzten Zeile der Tabelle werden noch die Summen aller Häufigkeiten bzw. der Gesamtschaden ermittelt.
2.3 Relative Bedeutung der Fehler
Prozentwerte berechnen
In diesem Schritt wird die relative Bedeutung der Fehler berechnet. Dazu drückt man die Häufigkeit des Auftretens jeder Fehlerart als Prozentsatz der Summe aller Häufigkeiten aus.
In diesem Schritt wird die relative Bedeutung der Fehler berechnet. Dazu drückt man die Häufigkeit des Auftretens jeder Fehlerart als Prozentsatz der Summe aller Häufigkeiten aus.
Für die Häufigkeiten geschieht dies mit folgender Formel:
Prozentwert | = | Häufigkeit der Fehlerart × 100 |
Summe aller Häufigkeiten |
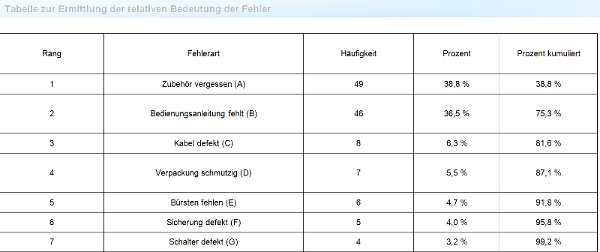
Eine tabellarische Darstellung erhöht die Übersicht und ermöglicht zugleich eine Eintragung gemäß der im vorhergehenden Schritt ermittelten Rangzahlen. Für obiges Beispiel ergibt sich Tabelle 2 (Werte gerundet).[ 07204_b.docx]
07204_b.docx]
 07204_b.docx]
07204_b.docx]Tabelle 2: Tabelle zur Ermittlung der relativen Bedeutung der Fehler
Rang | Fehlerart | Häufigkeit | Prozent | Prozent kumuliert |
|---|---|---|---|---|
1 | Zubehör vergessen (A) | 49 | 38,8 % | 38,8 % |
2 | Bedienungsanleitung fehlt (B) | 46 | 36,5 % | 75,3 % |
3 | Kabel defekt (C) | 8 | 6,3 % | 81,6 % |
4 | Verpackung schmutzig (D) | 7 | 5,5 % | 87,1 % |
5 | Bürsten fehlen (E) | 6 | 4,7 % | 91,8 % |
6 | Sicherung defekt (F) | 4,0 % | 95,8 % |
Kumulierte Prozente
In der letzten Spalte der Tabelle (Tab. 2) wurden auch gleich die Prozentzahlen kumuliert. Dies geschieht, indem der Prozentwert jeder Zeile zum kumulierten Prozentwert der Vorgängerzeile addiert wird. Mit den kumulierten Prozentzahlen wird später die Summenkurve gezeichnet.
In der letzten Spalte der Tabelle (Tab. 2) wurden auch gleich die Prozentzahlen kumuliert. Dies geschieht, indem der Prozentwert jeder Zeile zum kumulierten Prozentwert der Vorgängerzeile addiert wird. Mit den kumulierten Prozentzahlen wird später die Summenkurve gezeichnet.
2.4 Erstellung des Diagramms
Zwei Größenachsen
Zunächst müssen die passenden Achsen für das Diagramm erstellt werden. Auf der Abszisse werden die Fehlerkategorien abgetragen. Links und rechts der Abszisse werden zwei Ordinatenachsen benötigt: links für die absolute Häufigkeit des Auftretens einer Fehlerart, rechts eine zweite für die kumulierten Prozentwerte der Summenkurve.
Zunächst müssen die passenden Achsen für das Diagramm erstellt werden. Auf der Abszisse werden die Fehlerkategorien abgetragen. Links und rechts der Abszisse werden zwei Ordinatenachsen benötigt: links für die absolute Häufigkeit des Auftretens einer Fehlerart, rechts eine zweite für die kumulierten Prozentwerte der Summenkurve.
Übertragen der Werte
Die Werte aus der zweiten Tabelle (Tab. 2) werden nun in das Diagramm übertragen. Es gilt die Regel, dass die absoluten Häufigkeiten als Balken dargestellt werden, wohingegen die kumulierten Prozentwerte nur aus einer dünnen Kurvenlinie bestehen.
Die Werte aus der zweiten Tabelle (Tab. 2) werden nun in das Diagramm übertragen. Es gilt die Regel, dass die absoluten Häufigkeiten als Balken dargestellt werden, wohingegen die kumulierten Prozentwerte nur aus einer dünnen Kurvenlinie bestehen.
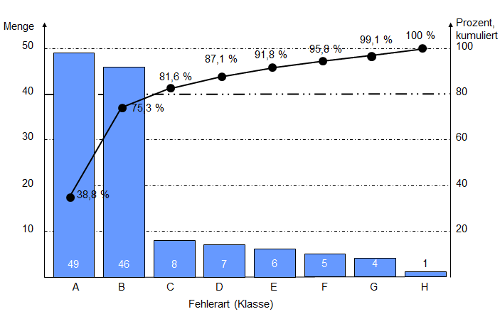
Abbildung 1 zeigt das fertige Diagramm. Die Buchstaben werden dabei zur Wahrung der Übersichtlichkeit benutzt. Sie finden das Beispiel auch als Powerpointdatei zum Download.[ 07204_c.pptx]
07204_c.pptx]
Abb. 1: Beispiel eines Pareto-Diagramms
 07204_c.pptx]
07204_c.pptx]2.5 Klassifikation der Wichtigkeit
80/20-Regel
Üblicherweise wird die Summenkurve auf der linken Seite des Diagramms rasch ansteigen und auf der rechten Seite immer flacher werden. In diesem typischen Verlauf manifestiert sich die 80/20-Regel von Pareto: Wenige Fehler (Ursachen) sind für einen Großteil der Probleme (Wirkungen) verantwortlich.
Üblicherweise wird die Summenkurve auf der linken Seite des Diagramms rasch ansteigen und auf der rechten Seite immer flacher werden. In diesem typischen Verlauf manifestiert sich die 80/20-Regel von Pareto: Wenige Fehler (Ursachen) sind für einen Großteil der Probleme (Wirkungen) verantwortlich.
In obigem Beispiel zeigt sich, dass allein durch die beiden Fehler A (Zubehör vergessen) und B (Bedienungsanleitung fehlt) über 75 % der Reklamationen verhindert werden könnten. Damit ist ein Ansatzpunkt gefunden, um schnell deutliche Verbesserungen zu erreichen.
Grenzen festlegen
Das Pareto-Diagramm identifiziert, welche Fehler in der Folge weiter betrachtet werden. Dazu wird auf Höhe der 80 %-Marke eine Hilfslinie eingezeichnet. Die Fehlerarten, die vor dem Schnittpunkt aus Summenkurve und Hilfslinie liegen, sind die wichtigen Fehler und sollen zunächst weiter betrachtet werden.
Das Pareto-Diagramm identifiziert, welche Fehler in der Folge weiter betrachtet werden. Dazu wird auf Höhe der 80 %-Marke eine Hilfslinie eingezeichnet. Die Fehlerarten, die vor dem Schnittpunkt aus Summenkurve und Hilfslinie liegen, sind die wichtigen Fehler und sollen zunächst weiter betrachtet werden.
3 Erfolgsfaktoren
Die Anwendung des Pareto-Diagramms ist einfach, sofern folgende Erfolgsfaktoren berücksichtigt werden:
Eindeutige Definitionen
Die Häufigkeit des Fehlerauftretens bestimmt den Verlauf der Summenkurve im Diagramm. Daher ist es wichtig, vor der Datenerhebung klar zu definieren, welcher Umstand als Fehler gewertet und welcher Kategorie er zugeordnet wird.
Die Häufigkeit des Fehlerauftretens bestimmt den Verlauf der Summenkurve im Diagramm. Daher ist es wichtig, vor der Datenerhebung klar zu definieren, welcher Umstand als Fehler gewertet und welcher Kategorie er zugeordnet wird.
Konsequenz beim Ergebnis
Das Pareto-Diagramm zeigt anhand von Zahlenwerten auf, mit welchen Fehlern man sich beschäftigen sollte, um das größte Potenzial zu heben. Der Anwender sollte sich diesen Fehlern zuwenden, auch wenn er oder das Team zunächst andere Fehler angehen wollten.
Das Pareto-Diagramm zeigt anhand von Zahlenwerten auf, mit welchen Fehlern man sich beschäftigen sollte, um das größte Potenzial zu heben. Der Anwender sollte sich diesen Fehlern zuwenden, auch wenn er oder das Team zunächst andere Fehler angehen wollten.
4 Vor- und Nachteile
Mit dem Pareto-Diagramm sind folgende Vor- und Nachteile verbunden:
| Vorteile | |
| • | Hilft beim rationellen Ressourceneinsatz, indem wichtige Fehler deutlich werden |
| • | Konzentriert Betrachtung auf wenige Fehler mit großem Potenzial |
| • | Kann Daten aus verschiedenen Quellen verwenden |
Nachteile
Eine reine Häufigkeitsbetrachtung kann die finanzielle Dimension eines Fehlers verschleiern.
Eine reine Häufigkeitsbetrachtung kann die finanzielle Dimension eines Fehlers verschleiern.
5 Fazit
Die Analyse eines Qualitätsproblems mit dem Pareto-Diagramm hilft, die Prioritäten für das weitere Vorgehen zu setzen. Seine Anwendung ist immer dann zu empfehlen, wenn knappe Ressourcen richtig eingesetzt werden sollen oder die Suche nach dem „richtigen” Ansatzpunkt andauert. Eine kurze Präsentation zu Schulungszwecken finden Sie diesem Beitrag als Arbeitshilfe zum Download angehängt.[ 07204_d.pptx]
07204_d.pptx]
 07204_d.pptx]
07204_d.pptx]Quellen
1
Rath & Strong's Six Sigma Pocket Guide. Werkzeuge zur Prozessverbesserung. Neue, überarb. Aufl. 2008. TÜV Media, Köln